Flocking-in-Fixed-and-Switching-Networks
Project maintained by yashsavle Hosted on GitHub Pages — Theme by mattgraham
Mini Project 2
Authors: Shubham Sonawane, Raj Shinde, Yash Savle, Moumita Paul
Introduction
We aim to implement the findings and results obtained in the paper “Flocking in Fixed and Switching Networks” by H. G. Tanner, A. Jadbabaie and G. J. Pappas, in IEEE Transactions on Automatic Control, vol. 52, no. 5, pp. 863-868, May 2007. doi: 10.1109/TAC.2007.895948.
The paper focuses on discussing the problem of planning for multi-agent robot navigation. Their approach is based on motion of biological groups of living beings. They present an algorothim which imitates the flocking model of the The authors have presented the performance of their flocking algorithm in this paper. In the results, it can be seen that the agents, which have different orientations initially, gradually align themselves. Also, the velocities of the agents can be seen to converge over a period of time. The three aspects which drive the actions of individual agents among the group are:
- Seperation: maintaining fixed distance between each other to avoid crowding.
- Alignment: Move along with the heading of local co-agents.
- Cohesion: Keep moving towards the average position of local co-agents.
Approach
The agents flocking in a group only consider a neighborhood in its vicinity. The region of the neighborhood is calculated with distance amongst the neighbors and angle from the direction of motion. In each neighborhood there is a leader present and all the robots will follow the three actions specified above. The number of interactions amongst th neighbors is pre determined. They then calculate the position, velocities and acceleration for the agents. Using these parameters te approach angle is calculated. The robots coordinate such that they try to achieve a common velocity and maintain fixed distance to avoid collisions. Lastly they define a set of control laws which govern the motion of the agents ina flock. We won’t discuss about the approach in depth as we focus on the simulation and results for this experiment.
Simulation
We have implemented the algorithm for a fixed network of agents. A fixed network means that the network is time invariant. We represent the communication network with the help of a graph. We have reproduced 2 results from the original paper, which are as follows:
- Demonstration of gradual orientation and position convergence of the agents
- Demonstration of velocity convergence of the agents
Our algorithm was tested on 10 agents, similar to the results presented in the paper.
The results are as follows:
- Initial state of the agents
The robots are moving in random direction without any control policy being employed on them
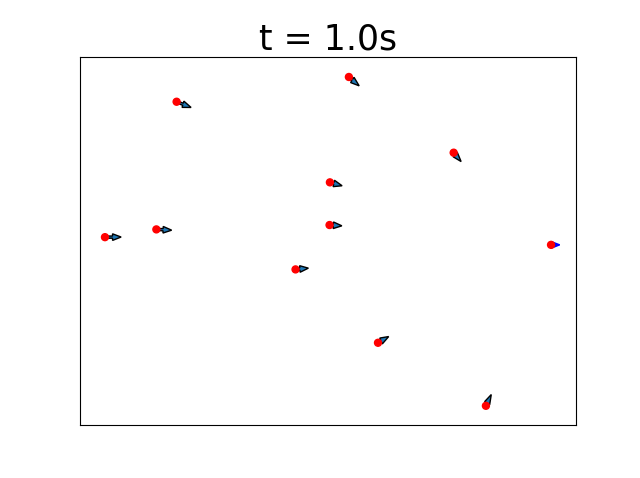
- Agent position and orientation after some time
As soon as we ran our algorithm for a duration of 1s we can see that a leader agent was chosen and other robots aligned themselves in the direction of the leader.
- Velocity convergence
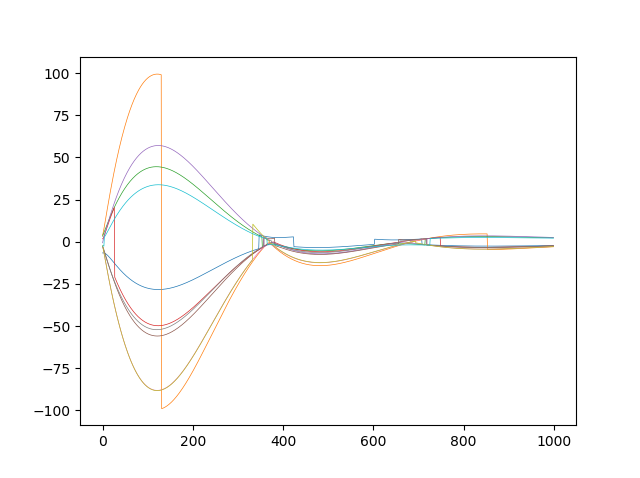
Our implementation does not take into account the maximum velocity limit for the agents. As seen from the graph above, the agents are able to change their velocity immediately. However, this will not be the case in real-world scenario.
The code for the implementation of this algorithm is available at: code
Future Work
The algorithm can be improved by incorporating the Dynamics of the robot as well as by considering the velocity and acceleration constraints in to account. This will help to predict actual behaviour for a fleet of drones.
References
[1] Flocking in Fixed and Switching Networks by H. G. Tanner, A. Jadbabaie and G. J. Pappas, in IEEE Transactions on Automatic Control, vol. 52, no. 5, pp. 863-868, May 2007. doi: 10.1109/TAC.2007.895948.
[2] C. W. Reynolds. Flocks, Herds and Schools: A Distributed Behavioral Model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH’87, pages 25–34, New York, NY, USA, 1987. ACM. doi:10.1145/37401.37406.
[3] [S. Zhou. Clone Swarms: Learning to Predict and Control Multi-Robot Systems by Imitation. In Proceedings of 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) ]
[4] R. Olfati-Saber Flocking for multi-agent dynamic systems: algorithms and theory. In proceedings of IEEE Transactions on Automatic Control March 2006